This page is out of date

You've reached a page on the Ren'Py wiki. Due to massive spam, the wiki hasn't been updated in over 5 years, and much of the information here is very out of date. We've kept it because some of it is of historic interest, but all the information relevant to modern versions of Ren'Py has been moved elsewhere.

Some places to look are:

Please do not create new links to this page.

Springy movement

If you want to add some spring to your Moves, the following code might be what you’re looking for. It’s based on the under-damped response to a step input, which is gradually decaying oscillations. I’m going to offer two different ways of doing it – one simple and one more complex that offers more options.

movement-profile-springy.png

General information

The equation used is basically x(t) = 1 - ℯ^-ρtcos(μt) (which is then divided by a scaling factor). It takes two parameters that you can use to tweak the motion: ρ and μ.

Avoiding singularities

You can set these two parameters to any values that you like, as long as the following equation isn’t true:

ℯ^ρ = cos(μ)

This is because of the scaling factor used, and it means that you have selected values of ρ and μ that leave you back where you started when the springing is done. You’ll know if you’ve picked this combination if you get a divide by zero error, but the only way you can manage that is if ρ is less than or equal to zero. So as long as you keep ρ greater than zero, you won’t have to worry about that.

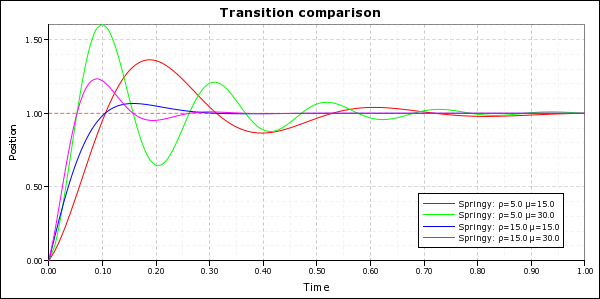
What `ρ` does

ρ controls the decay rate, or how fast the bounces dissipate. The higher you set ρ, the faster the bounciness vanishes as it settles. If you set ρ too low, it will still be bouncing at the end of the Move, and it will seem to come to an abrupt halt.

You can set ρ to a negative number, which means increasing oscillations, as if it is in resonance. I don’t know why you’d want to do this – but if you want to, that’s how.

If you make ρ large: The motion will start more abruptly and the bouncing will end more quickly.
If you make ρ small, but greater than zero: The motion will start more smoothly and the bouncing will take longer to end (and might not end before the time’s up, which will mean an abrupt finish).
If you make ρ zero or negative: The motion will start smoothly but the bouncing will get bigger or stay the same size instead of getting smaller. You also run the risk of a singularity.

What `μ` does

μ controls the bounce frequency, or how many bounces happen during the move.

If you make μ large (positive or negative): The motion will start more abruptly and you will get more bounces.
If you make μ small (positive or negative) or zero: The motion will start more smoothly, and you will get less bounces (or none at all).

Simple form

The simplest way to use the bounce formula is as a time warp function to Move.

import math

def springy_time_warp_real(x, rho, mu):
  return (1.0 - math.exp(-rho * x) * math.cos(mu * x)) / (1.0 - math.exp(-rho) * math.cos(mu))

springy_time_warp = renpy.curry(springy_time_warp_real)

And to use it:

show eileen happy at Move(offscreenleft, center, 1.0, time_warp = springy_time_warp(rho = 5.0, mu = 15.0))

Optimizing

If you have selected a ρ and μ that you like, and you don’t intend to change them, you can simplify the equation a bit to get a speed increase. The best way to do that is to start out with the following code:

import math

rho = 5.0
mu = 15.0
scale_factor = 1.0 - math.exp(-rho) * math.cos(mu)

def springy_time_warp(x):
  return (1.0 - math.exp(-rho * x) * math.cos(mu * x)) / scale_factor

...

show eileen happy at Move(offscreenleft, center, 1.0, time_warp = springy_time_warp)

Use that code during development, so you can tweak ρ and μ until you’re ready to release. Then replace ρ and μ with your chosen values, and scale_factor with 1 – ℯ^–ρcos(μ).

Complex form

Now the simple form does the job most of the time, but it has some limitations. The nature of the motion means that it can be pretty abrupt when it starts for certain values. You can use time warp functions to smooth this out, but not with the simple form. Another benefit of the complex form is that it is already optimized, and doesn’t require editing before release.

class UnderdampedOscillationInterpolater(object):
   
    anchors = {
        'top' : 0.0,
        'center' : 0.5,
        'bottom' : 1.0,
        'left' : 0.0,
        'right' : 1.0,
        }
   
    def __init__(self, start, end, rho, mu):
       
        import math
       
        if len(start) != len(end):
            raise Exception("The start and end must have the same number of arguments.")
       
        self.start = [ self.anchors.get(i, i) for i in start ]
        self.end = [ self.anchors.get(i, i) for i in end ]
        self.rho = rho
        self.mu = mu
        self.c = 1.0 - math.exp(-rho) * math.cos(mu)
   
    def __call__(self, t, sizes=(None, None, None, None)):
       
        import math
       
        t = (1.0 - math.exp(-self.rho * t) * math.cos(self.mu * t)) / self.c
       
        def interp(a, b, c):
           
            if c is not None and isinstance(a, float):
                a = int(a * c)
           
            if c is not None and isinstance(b, float):
                b = int(b * c)
           
            rv = (b - a) * t + a
           
            if isinstance(a, int) and isinstance(b, int):
                return int(rv)
            else:
                return rv
       
        return [ interp(a, b, c) for a, b, c in zip(self.start, self.end, sizes) ]

def Springy(startpos, endpos, time, rho, mu, child=None, repeat=False, bounce=False, anim_timebase=False, style='default', time_warp=None, **properties):
   
    return Motion(UnderdampedOscillationInterpolater(startpos, endpos, rho, mu), time, child, repeat=repeat, bounce=bounce, anim_timebase=anim_timebase, style=style, time_warp=time_warp, add_sizes=True, **properties)

And you use it with:

show eileen happy at Springy(offscreenleft, center, 1.0, 5.0, 15.0)